Mode Sleep Bisa Bikin Baterai Laptop Cepat Habis ?

Dalam button power ada 3 pilihan metode untuk mulai proses di sebuah sistem operasi

Ada mitos nih katanya kalau kita memilih mode sleep pada saat ingin meninggalkan pekerjaan di Laptop , baterai kita akan lebih cepat habis. Apakah itu benar ? Simak ulasan berikut ini

• Mode sleep tidak begitu berpengaruh pada baterai 

Faktanya hanya sekitar 1-3 watt listrik yang terpakai ketika menggunakan mode sleep.

• File akan tersimpan di RAM

Seluruh file yang aktif saat itu dan program yang bekerja akan tersimpan sementara di RAM

• Kinerja Laptop akan terasa berat

Saat baterai laptop krisis, maka mode hibernasi akan aktif secara otomatis , yang paling mungkin terjadi adalah kinerja laptop akan semakin berat jika lama tidak di matikan.

Nah jadi itu hanya mitos teknologi, ada beberapa perspektif tentang sleepmode dan shutdown pada laptop. Kalian lebih pilih yang mana ?

      

Read More

Komponen arsitektur sistem pendukung keputusan (DSS)

Pengertian DSS 

Sistem Pendukung Keputusan (SPK) atau Decision Support System (DSS) adalah sebuah sistem yang mampu memberikan kemampuan pemecahan masalah maupun kemampuan pengkomunikasian untuk masalah dengan kondisi semi terstruktur dan tak terstruktur. Sistem ini digunakan untuk membantu pengambilan keputusan dalam situasi semi terstruktur dan situasi yang tidak terstruktur, dimana tak seorangpun tahu secara pasti bagaimana keputusan seharusnya dibuat (Turban, 2001).

Sprague dan Watson mendefinisikan Sistem Pendukung Keputusan (SPK) sebagai sistem yang memiliki lima karakteristik utama yaitu (Sprague et.al, 1993):

1. Sistem yang berbasis komputer. 
2. Dipergunakan untuk membantu para pengambil keputusan 
3. Untuk memecahkan masalah-masalah rumit yang mustahil dilakukan dengan kalkulasi manual 
4. Melalui cara simulasi yang interaktif 
5. Dimana data dan model analisis sebaai komponen utama.

 Komponen Sistem Pendukung Keputusan

Secara umum Sistem Pendukung Keputusan dibangun oleh tiga komponen besar yaitu database Management, Model Base dan Software System/User Interface. Komponen SPK tersebut dapat digambarkan seperti gambar di bawah ini.

Penjelasan :

1. Subsistem data (database), merupakan tempat untuk menyimpan data yang relevan bagi sistem dan diorganisasikan oleh suatu sistem dengan manajemen database (Database Management System/DBMS) sehingga data dapat diekstrasi dengan cepat. Data berasal dari sumber internal (dari dalamperusahaan) dan eksternal (dari luar perusahaan). Kemampuan yang dibutuhkan dari suatu manajemen database (Suryadi, 1998), yaitu :

• Kemampuan untuk mengkombinasikan berbagai variasi data melalui pengambilan dan ekstraksi data. 
• Kemampuan untuk menambahkan sumber data secara cepat dan mudah. 
• Kemampuan untuk menggambarkan struktur data logikal sesuai dengan pengertian pemakai, sehingga pemakai mengetahui apa yang tersedia dan dapat menestukan kebutuhan penambahan dan pengurangan. 
• Kemampuan untuk menangani data secara personil, sehingga pemakai dapat mencoba berbagai alternatif pertimbangan personil. 
• Kemampuan untuk mangelola berbagai variasi data. 

2. Subsistem model (modelbase), digunakan untuk menggambarkan data dalam suatu model untuk memudahkan pemrosesan data tersebut. Salah satu keunggulan SPK adalah memiliki kemampuan untuk mengintegrasikan akses data dan model-model keputusan. Yaitu dengan menambahkan model-model keputusan kedalam sistem informasi yang menggunakan database sebagai mekanisme integrasi dan komunikasi di antara model-model. Model merupakan peniruan dari permasalahn yang sebenarnya. Namun dalam prosesnya, sering kali model yang dirancang tidak mampu mencerminkan seluruh variabel dari permasalahn sebenarnya, sehingga keputusan yang diambil berdasarkan model menhadi tidak akurat dan tidak sesuai dengan kebutuhan. Oleh karena itu, model yang dirancang menggunakan koleksi berbagai model yang terpisah, dimana setiap model digunakan untuk menangani bagian berbeda dari masalah yang sedang dihadapi. Selain itu, model juga harus fleksibel, yaitu harus ada fasilitas yang mampu membantu pengguana untuk memodifikasi dan menyempurnakan model sesuai dengan perkembangan zaman. Kemampuan yang dimiliki subsistem basis model (Suryadi, 1998), yaitu :

• Kemampuan utnuk menciptakan model-model baru secara cepat dan mudah.
• Kemampuan untuk mengakses dan mengintegrasikan model-model keputusan.
• Kemampuan untuk mengelola basis model dengan fungsi manajemen yang analog dan manajemen database, seperti mekanisme untuk menyimpan, membuat dialog, menghubungkan, dan mengakses model.

3. Subsistem dialog (user system interface), berfungsi sebagai perantara antara sistem dengan user. Inilah keunikan lain pada SPK, yaitu mampu mengintegrasikan sistem terpasang dengan pengguna secara interaktif. Subsistem dialog menengartikulasikan dan mengimplementasikan sistem sehingga pengguna dapat berkomunikasi dengan sistem yang dirancang. Subsistem ini dibagi menjadi tiga komponen (Daihani, 2001), yaitu :

• Bahasa aktif (Action Language), perangkat yang digunakan untuk berkomunikasi dengan sistem, seperti keyboard, joystick, panel-panel sentuh lain, perintah suara atau key function lainnya. 
• Bahasa tampilan (Presentation Language), perangkat yang digunakan sebagai sarana untuk menampilkan sesuatu, seperti printer, grafik display, plotter, dan lainnya.
• Bahasa pengetahuan (Knowladge Language), perangkat yang harus diketahui pengguna agar pemakaian sistem bisa efektif. Basis pengetahuan dapat diperoleh dari buku, artikel, petunjuk ahli, ataupun pemikiran dari pengguna sendiri.

Kombinasi dan kemampuan di atas terdiri dari apa yang disebut gaya dialog, misalnya meliputi pendekatan tanya jawab, bahasa perintah, menu-menu, dan mengisi tempat yang kosong. Kemampuan yang harus dimiliki SPK untuk mendukung dialog sistem (Suryadi, 1998), yaitu :

• Kemampuan untuk menangani berbagai variasi gaya dialog. Bahkan jika mungkin untuk mengkombinasikan berbagai gaya dialog sesuai dengan pilihan pemakai. 
• Kemampuan untuk mengakomodasi tindakan pemakai dengan berbagai peralatan masukan.
• Kemampuan untuk menampilkan data dengan berbagai variasi format dan peralatan keluaran. 
• Kemampuan untuk memberikan dukungan yang fleksibel untuk mengetahui basis pengetahuan pemakai. 

Read More

Pengertian Kunci Algoritma RSA

RSA

Salah satu algoritma kriptografi kunci-nirsimetri (kunci-publik) yang paling terkenal adalah RSA (Rivest, Shamir, Adleman). Algoritma ini dibuat oleh Ron Rivest, Adi Shamir, dan Leonard Adleman. Keamanan algoritma RSA terletak pada sulitnya memfaktorkan bilangan yang besar menjadi faktorfaktor prima. Pemfaktoran ini dilakukan untuk memperoleh kunci rahasia. Selama pemfaktoran bilangan besar menjadi faktor-faktor prima belum ditemukan algoritma maka selama itu pula keamanan algoritma RSA tetap terjamin [MUN06].

Untuk membangkitkan pasangan kunci (kunci publik dan kunci rahasia), beberapa langkah yang harus dilakukan antara lain:
1. Pilih dua bilangan prima sembarang p dan q
2. Hitung n = p.q. Sebaiknya p ≠ q maka n = p2 sehingga p dapat diperoleh dengan menarik akar kuadrat dari n
3. Hitung φ(n) = (p - 1).(q - 1)
4. Pilih kunci publik e yang relatif prima terhadap φ(n)
5. Bangkitkan kunci rahasia d dengan persamaan:
e.d ≡ 1 (mod φ(n)) ..............................................(1)
Perhatikan bahwa persamaan diatas ekivalen dengan e.d ≡ 1 + k φ(n), sehingga d dapat dihitung dengan:
d = (1 + k φ(n))/e .............................................(2)
Disini akan didapat dua hasil perhitungan yaitu pasangan n dan d sebagai kunci rahasia (private) dan pasangan n dan e sebagai kunci publik yang sifatnya tidak rahasia [MUN06].

Untuk mengenkripsi pesan (plainteks) menjadi cipherteks, langkah-langkah yang dilakukan adalah:
1. Ambil kunci penerima pesan e dan modulus n 

2. Nyatakan plainteks m menjadi blok-blok m1, m2, ... sedemikian sehingga setiap blok merepresentasikan nilai dalam selang [0,n-1]
3. Setiap blok mi dienkripsi menjadi blok ci dengan rumus
E m c me n
e i i i ( ) = ≡ mod ........................ ..............(3)
Sedangkan untuk dekripsi digunakan rumus:
D c m cd n
d i i i ( ) = = mod ..................................... (4)
Kekuatan algoritma RSA ini terletak pada sulitnya memfaktorkan suatu bilangan yang besar menjadi faktor primanya. Sehingga semakin panjang pasangan kunci yang digunakan (dalam artian semakin besar bilangan kuncinya) maka algoritma RSA akan semakin aman.

Read More

Proses Enkripsi Permutasi DES (Data Encryption Standard)

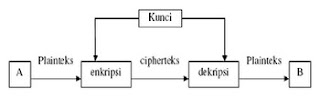
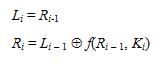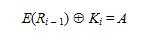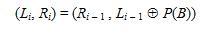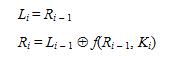Algoritma DES (Data Encryption Standard)
Sebagai salah satu sistem kriptografi simetris, DES tergolong jenis cipher blok. DES dikatakan enkripsi blok karena pemrosesan data baik enkripsi maupun dekripsi, diimplementasikan per blok (dalam hal ini 8 byte). Proses pada algoritma DES terbilang panjang, bahkan jauh lebih panjang daripada Elgamal, tapi pada implementasinya ternyata proses komputasinya dapat berjalan lebih cepat. Mengapa demikian? karena pada DES tidak ada operasi aritmatika yang berjalan seperti halnya pada Elgamal. Proses yang berjalan pada DES hanya sebatas pergeseran bit-bit pada tiap blok enkripsi/dekripsi.
Pertama yang harus kita ketahui dari algoritma ini adalah Skema global yang ada pada algoritma DES, diuraikan sebagai berikut:
a.    Blok plainteks dipermutasi dengan permutasi awal (IP, Initial Permutation).
b.    Hasil permutasi awal kemudian dienciphering sebanyak 16 kali (16 putaran). Setiap putaran menggunakan kunci internal yang berbeda dengan perhitungan LiRi dengan 1 ≤ i ≤ 16.
c.    Hasil enciphering kemudian dipermutasi dengan matriks permutasi balikan (invers initial  permutation atau IP-1) menjadi blok cipherteks.
Permutasi Awal (Initial Permutation)
Sebelum putaran pertama, terhadap blok plainteks dilakukan permutasi awal (Initial Permutation atau IP). Tujuan permutasi awal adalah mengacak plainteks sehingga urutan-bit-bit di dalamnya berubah. Lihat pada gambar dibawah, Matriks pada Tabel (a) sebagai plainteks masukan, kemudian dilakukan pengacakan dengan menggunakan matriks permutasi awal Tabel (b):

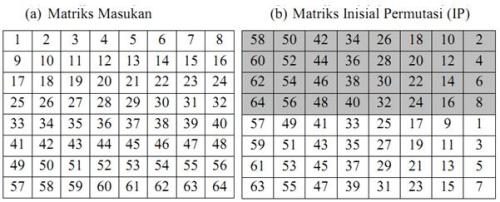
Setelah melewati Permutasi Awal, plainteks yang akan disandikan kemudian dibagi menjadi dua blok (ditunjukkan dengan warna yang berbeda pada Tabel (b)), yaitu blok atas dan blok bawah yang masing‐masing lebarnya 4 byte (32-bit).
Pembangkitan Kunci Internal DES
Pada algoritma DES, dibutuhkan kunci internal sebanyak 16 buah, yaitu K1, K2,…,K16. Kunci-kunci internal ini dapat dibangkitkan sebelum proses enkripsi atau bersamaan dengan proses enkripsi. Kunci internal dibangkitkan dari kunci eksternal yang diberikan oleh pengguna. Kunci eksternal pada DES panjangnya 64-bit atau 8 karakter seperti pada Tabel (c) dibawah.

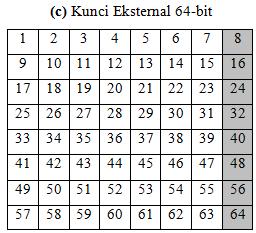
Misalkan kunci eksternal yang tersusun atas 64-bit adalah K. Kunci eksternal ini menjadi masukan untuk permutasi dengan menggunakan matriks kompresi PC-1 seperti pada Tabel (d).

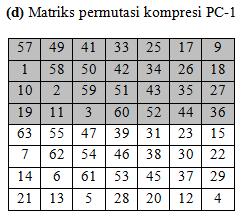
Dalam permutasi ini, tiap-bit kedelapan dari delapan byte kunci diabaikan (Tabel (c) dengan kolom yang berwarna gelap). Hasil permutasinya adalah sepanjang 56-bit, sehingga dapat dikatakan panjang kunci DES adalah 56-bit.
Selanjutnya, 56-bit ini dibagi menjadi 2 bagian, atas dan bawah, yang masing-masing panjangnya 28-bit, dan masing-masing disimpan di dalam C0 dan D0.
C0:  berisi-bit-bit dari K pada sisi gelap tabel (d)
D0:  berisi-bit-bit dari K pada sisi putih tabel (d)
Selanjutnya, kedua bagian digeser ke kiri (left shift) sepanjang satu atau dua-bit bergantung pada tiap putaran. Jumlah pergeseran pada tiap putaran ditunjukkan pada Tabel (e).

Misalkan (Ci, Di) menyatakan penggabungan Ci dan Di. (Ci-1, Di-1) diperoleh dengan menggeser Ci dan Di satu atau dua-bit. Setelah Pergeseran-bit, (Ci, Di) mengalami permutasi kompresi dengan menggunakan matriks PC-2 seperti pada Tabel (f).

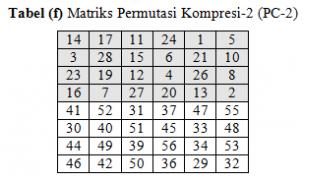
Dengan permutasi ini, kunci internal Ki diturunkan dari (Ci, Di) yang dalam hal ini Ki merupakan panggabungan-bit-bit Ci pada sisi gelap tabel (f), dengan-bit-bit Di pada sisi putih tabel (f).
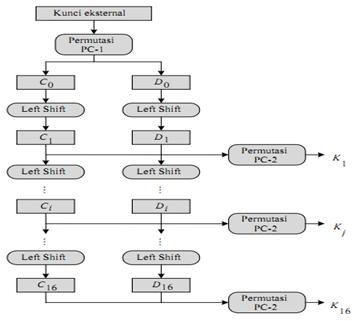
Setiap kunci internal Ki mempunyai panjang 48-bit. Proses Pembangkitan kunci-kunci internal dapat dilihat pada gambar berikut ini :

Proses Enkripsi DES
Proses enkripsi terhadap blok plainteks dilakukan setelah permutasi awal. Setiap blok plainteks mengalami 16 kali putaran enkripsi. Untuk setiap putaran, digambarkan seperti gambar berikut :

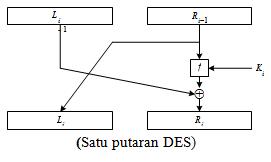
Setiap putaran enkripsi DES secara matematis dinyatakan sebagai :

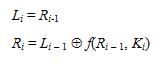
Dengan  f adalah suatu fungsi yang ditunjukkan pada Gambar berikut :

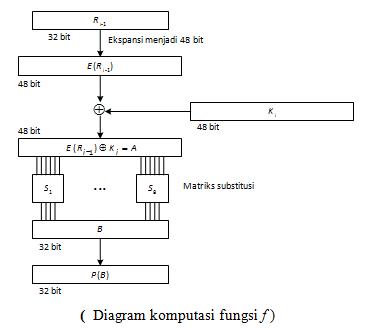
E adalah fungsi ekspansi yang memperluas blok Ri – 1 32-bit menjadi blok 48-bit. Fungsi ekspansi direalisasikan dengan matriks permutasi ekspansi :

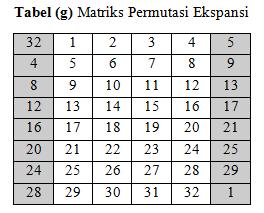
Hasil ekpansi, yaitu E(Ri – 1) di-XOR-kan dengan Ki menghasilkan vektor A 48-bit:

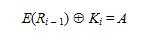
Matriks A dikelompokkan menjadi 8 kelompok, masing-masing 6-bit, dan menjadi masukan bagi proses substitusi. Proses substitusi dilakukan dengan menggunakan delapan buah kotak-S (S-box), S1 sampai S8. Setiap kotak-S menerima masukan 6-bit dan menghasilkan keluaran 4-bit. Kelompok 6-bit pertama menggunakan S1, kelompok 6-bit kedua menggunakan S2, dan seterusnya. Kedelapan kotak-S tersebut ditunjukkan pada gambar di bawah ini (klik untuk memperbesar).

Keluaran proses substitusi adalah vektor B yang panjangnya 32-bit. Vektor B menjadi masukan untuk proses permutasi. Tujuan permutasi adalah untuk mengacak hasil proses substitusi kotak-S. Permutasi dilakukan dengan menggunakan matriks permutasi P (P-box) sbb :

Bit-bit P(B) merupakan keluaran dari fungsi f.
Akhirnya, bit-bit P(B) di-XOR-kan dengan Li–1 untuk mendapatkan Ri
Jadi, keluaran dari putaran ke-i adalah


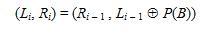
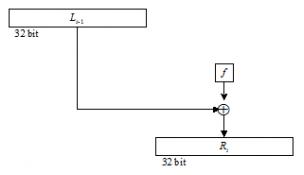
Skema perolehan Ri
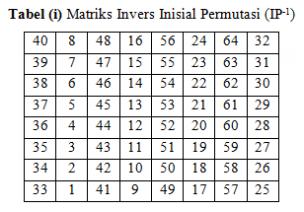
Permutasi Akhir (Invers Inisial Permutasi)
Permutasi terakhir dilakukan setelah 16 kali putaran terhadap gabungan  blok kiri dan blok kanan. Permutasi menggunakan matriks permutasi awal balikan (IP-1 ) sbb:

Proses Dekripsi DES
Proses dekripsi terhadap cipherteks merupakan kebalikan dari proses enkripsi. DES menggunakan algoritma yang sama untuk proses enkripsi dan dekripsi. Jika pada proses enkripsi urutan kunci internal yang digunakan adalah K1, K2, …, K16, maka pada proses dekripsi urutan kunci yang digunakan adalah K16, K15, …, K1. Setiap putaran 16, 15, …, 1, keluaran pada proses dekripsi adalah

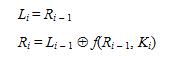
dalam hal ini, (R16, L16) adalah blok masukan awal untuk proses dekripsi.
Blok (R16, L16) diperoleh dengan mempermutasikan cipherteks dengan matriks permutasi IP. Pra-keluaran dari proses dekripsi adalah adalah (L0, R0). Dengan permutasi awal IP-1 akan didapatkan kembali blok plainteks semula. Kunci-kunci dekripsi diperoleh dengan menggeser Ci dan Di dengan cara yang sama seperti pada proses enkripsi, tetapi pergeseran kiri (left shift) diganti menjadi pergeseran kanan (right shift).

Read More

Pengertian dan contoh teknik Dasar kriptografi

Teknik Dasar Kriptografi Terbagi 5 Jenis, yaitu :
1. Substitusi
2. Blocking
3. Permutasi
4. Ekspansi
5. Pemampatan


Lanjut Ke penjelasan Dan Contohnya :

1. SUBSTITUSI

Dalam kriptografi, sandi substitusi adalah jenis metode enkripsi dimana setiap satuan pada teks terang digantikan oleh teks tersandi dengan sistem yang teratur. Metode penyandian substitusi telah dipakai dari zaman dulu (kriptografi klasik) hingga kini (kriptografi modern),
Langkah pertama adalah membuat suatu tabel substitusi. Tabel substitusi dapat dibuat sesuka hati, dengan catatan bahwa penerima pesan memiliki tabel yang sama untuk keperluan decrypt.  Bila tabel substitusi dibuat secara acak, akan semakin sulit pemecahanciphertext oleh orang yang tidak berhak.
Metode ini dilakukan dengan mengganti setiap huruf dari teks asli dengan huruf lain sebagai huruf sandi yang telah didefinisikan sebelumnya oleh algoritma kunci.

Contoh:
Metode Penyandian Substitusi Sederhana

2. BLOCKING
Sistem enkripsi ini terkadang membagi plaintext menjadi beberapa blok yang terdiri dari beberapa karakter, kemudian di enkripsikan secara independen.

Caranya :
Plaintext dituliskan secara vertikal ke bawah berurutan pada lajur, dan dilanjutkan pada kolom berikutnya sampai seluruhnya tertulis. Ciphertext-nya adalah hasil pembacaan plaintext secara horizontal berurutan sesuai dengan blok-nya.

Contoh :

3. PERMUTASI
Salah satu teknik enkripsi yang terpenting adalah permutasi atau sering juga disebut transposisi. Teknik ini memindahkan atau merotasikan karakter dengan aturan tertentu. Prinsipnya adalah berlawanan dengan teknik substitusi. Dalam teknik substitusi, karakter berada pada posisi yang tetap tapi identitasnya yang diacak. Pada teknik permutasi, identitas karakternya tetap, namun posisinya yang diacak.

Caranya
Sebelum dilakukan permutasi, umumnya plaintext terlebih dahulu dibagi menjadi blok-blok dengan panjang yang sama.
Plaintext akan dibagi menjadi blok-blok yang terdiri dari 6 karakter, dengan aturan permutasi, sebagai berikut :

4. EKSPANSI
Suatu metode sederhana untuk mengacak pesan adalah dengan memelarkan pesan itu dengan aturan tertentu.  Salah satu contoh penggunaan teknik ini adalah dengan meletakkan huruf konsonan atau bilangan ganjil yang menjadi awal dari suatu kata di akhir kata itu dan menambahkan akhiran “an”. Jika suatu kata dimulai dengan huruf vokal atau bilangan genap, ditambahkan akhiran “i”.
Contoh :

5. PEMAMPATAN
Mengurangi panjang pesan atau jumlah bloknya dengan cara lain untuk menyembunyikan isi pesan.
Contoh sederhana ini menggunakan cara menghilangkan setiap karakter ke-tiga secara berurutan. Karakter-karakter yang dihilangkan disatukan kembali dan disusulkan sebagai “lampiran” dari pesan utama, dengan diawali oleh suatu karakter khusus, dalam contoh ini menggunakan ”  * “.

Contoh :

 

PERMUTASI , EKSPANSI,PEMAMPATAN

  

Read More

Teknik susbtitusi vigenere beserta contohnya

Kode vigènere termasuk kode abjad-majemuk (polyalphabetic substitution cipher). Dipublikasikan oleh diplomat (sekaligus seorang kriptologis) Perancis, Blaise de Vigènere pada abad 16, tahun 1586. Sebenarnya Giovan Batista Belaso telah menggambarkannya untuk pertama kali pada tahun 1533 seperti ditulis di dalam buku La Cifra del Sig. Algoritma ini baru dikenal luas 200 tahun kemudian dan dinamakan kode vigènere. Vigènere merupakan pemicu perang sipil di Amerika dan kode vigènere digunakan oleh Tentara Konfederasi (Confederate Army) pada perang sipil Amerika (American Civil War). Kode vigènere berhasil dipecahkan oleh Babbage dan Kasiski pada pertengahan abad 19. (Ariyus, 2008).

Algoritma enkripsi jenis ini sangat dikenal karena mudah dipahami dan diimplementasikan. Teknik untuk menghasilkan ciphertext bisa dilakukan menggunakan substitusi angka maupun bujursangkar vigènere. Teknik susbtitusi vigènere dengan menggunakan angka dilakukan dengan menukarkan huruf dengan angka, hampir sama dengan kode geser. Contoh:

Gambar 1 Contoh Tabel Substitusi Algoritma Kriptografi Vigenere Cipher

Plaintext: PLAINTEXT

Kunci: CIPHER

Gambar 2 Contoh Tabel Kriptografi dengan Algoritma Vigenere Cipher

Dengan metode pertukaran angka dengan huruf di atas, diperoleh bahwa teks asli (PLAINTEXT) memiliki kode angka (15,11, 0, 8, 13, 19, 4, 23, 19), sedangkan kode angka untuk teks kunci (CIPHER) yaitu (2, 8, 15, 7, 4, 17). Setelah dilakukan perhitungan, maka dihasilkan kode angka ciphertext (17, 19, 15, 15, 17, 10, 6, 5, 8). Jika diterjemahkan kembali menjadi huruf sesuai urutan awal, maka menjadi huruf RTPPRKGFI.

Sedangkan metode lain untuk melakukan proses enkripsi dengan metode vigènere cipher yaitu menggunakan tabula recta (disebut juga bujursangkar vigènere).

Gambar 3 Contoh Tabula Recta Algoritma Kriptografi Vigenere Cipher

 Kolom paling kiri dari bujursangkar menyatakan huruf-huruf kunci, sedangkan baris paling atas menyatakan huruf-huruf plaintext. Setiap baris di dalam bujursangkar menyatakan huruf-huruf ciphertert yang diperoleh dengan Caesar cipher, yang mana jumlah pergeseran huruf plaintext ditentukan nilai numerik huruf kunci tersebut (yaitu, a=0, b=1, c=2, …, z=25). Sebagai contoh, huruf kunci c (=2) menyatakan huruf-huruf plaintext digeser sejauh 2 huruf ke kanan (dari susunan alfabetnya), sehingga huruf-huruf ciphertext pada baris c adalah:

Gambar 4 Potongan Tabula Recta Baris ke-C

Bujursangkar vigènere digunakan untuk memperoleh ciphertert dengan menggunakan kunci yang sudah ditentukan. Jika panjang kunci lebih pendek daripada panjang plaintext, maka kunci diulang penggunaannya (sistem periodik). Bila panjang kunci adalah m, maka periodenya dikatakan m. Sebagai contoh, jika plaintext adalah THIS PLAINTEXT dan kunci adalah sony, maka penggunaan kunci secara periodik sebagai berikut:

Plaintext : THIS PLAINTEXT

Kunci     : sony sonysonys

Untuk mendapatkan ciphertext dari teks dan kunci di atas, untuk huruf plaintext pertama T, ditarik garis vertikal dari huruf T dan ditarik garis mendatar dari huruf s, perpotongannya adalah pada kotak yang berisi huruf L. Dengan cara yang sama, ditarik garis vertikal dari huruf H dan ditarik garis mendatar pada huruf o, perpotongannya adalah pada kotak yang juga berisi berisi huruf V. hasil enkripsi seluruhnya adalah sebagai berikut:

Plaintext             : THIS PLAINTEXT

Kunci                 : sony sonysonys

Ciphertext          : LVVQ HZNGFHRVL

Variasi-variasi vigènere cipher pada dasarnya perbedaannya terletak pada cara membentuk tabel atau cara menghasilkan kuncinya, sedangkan enkripsi dan dekripsi tidak berbeda dengan vigènere cipher standar. Beberapa variasi tersebut sebagai berikut:

1.    Full Vigènere Cipher

Pada varian ini, setiap baris di dalam tabel tidak menyatakan pergeseran huruf, tetapi merupakan permutasi huruf-huruf alfabet. Misalnya, pada baris a susunan huruf-huruf alfabet adalah acak seperti di bawah ini:

Gambar 5 Contoh Potongan Tabula Recta Full Vigenere Cipher

2.    Auto-Key Vigènere cipher

Idealnya kunci tidak digunakan secara berulang. Pada auto-key vigènere cipher, jika panjang kunci lebih kecil dari panjang plaintext, maka kunci disambung dengan plaintext tersebut. Misalnya, untuk mengenkripsi pesan NEGARA PENGHASIL MINYAK dengan kunci INDO, maka kunci tersebut disambung dengan plaintext semula sehingga panjang kunci menjadi sama dengan panjang plaintext:

Plaintext: NEGARA PENGHASIL MINYAK

Kunci: INDONE GARAPENGH ASILMI

3.    Running-Key Vigènere cipher

Pada varian ini, kunci bukan string pendek yang diulang secara periodik seperti pada vigènere cipher standar, tetapi kunci adalah string yang sangat panjang yang diambil dari teks bermakna (misalnya naskah proklamasi, naskah Pembukaan UUD 1945, terjemahan ayat di dalam kitab suci, dan lain-lain). Misalnya untuk mengenkripsi plaintext NEGARA PENGHASIL MINYAK dapat menggunakan kunci berupa sila ke-2 Pancasila: KEMANUSIAAN YANG ADIL DAN BERADAB. Selanjutnya enkripsi dan dekripsi dilakukan seperti biasa. (Munir, 2006)

AUTOKEY VIGENERE

VIGENERE CHIPER

Read More

Pengertian dan jenis kriptografi klasik beserta contohnya

Dalam kriptografi, pesan atau informasi yang dapat dibaca disebut sebagai plaintext atau clear text. Proses yang dilakukan untuk mengubah plaintext ke dalam ciphertext disebut enkripsi. Pesan yang tidak dapat terbaca tersebut disebut ciphertext. Proses yang merupakan kebalikan dari enkripsi disebut sebagai dekripsi. Proses ekripsi dapat digunakan untuk membuat ciphertext kembali menjadi plaintext. Ahli di bidang kriptografi disebut sebagai cryptographer. Cryptanalyst merupakan orang yang melakukan cryptanalysis, yaitu seni dan ilmu untuk memecahkan ciphertext menjadi plaintext tanpa melalui cara yang seharusnya. Sebelum komputer ada, kriptografi dilakukan dengan menggunakan pensil dan kertas. Algoritma kriptografi (cipher) yang digunakan saat itu, dinamakan juga algoritma klasik, adalah berbasis karakter, yaitu enkripsi dan dekripsi dilakukan pada setiap karakter pesan. Semua algoritma klasik termasuk ke dalam sistrm kriptografi simetris dan digunakan jauh sebelum kriptografi kunci publik ditemukan.

Kriptogarfi klasik memiliki beberapa ciri :

1. Berbasis karakter
2. Menggunakan pena dan kertas saja, belum ada computer
3. Termasuk ke dalam kriptografi kunci simetris.

Tiga alasan mempelajari algoritma klasik :

1. Memahami konsep dasar kriptografi
2. Dasar algoritma kriptografi modern
3. Memahami kelemahan sistem kode

Pada dasarnya, algoritma kriptografi klasik dapat dikelompokkan ke dalam dua macam cipher, yaitu :

1. Cipher substitusi (substitution cipher)
Di dalam cipher substitusi setiap unit plainteks diganti dengan satu unit cipherteks. Satu “unit” di isini berarti satu huruf, pasanga huruf, atau dikelompokkan lebih dari dua huruf. Algoritma substitusi tertua yang diketahui adalah Caesar cipher yang digunakan oleh kaisar Romawi , Julius Caesar (sehingga dinamakan juga casear cipher), untuk mengirimakan pesan yang dikirimkan kepada gubernurnya.
2. Cipher transposisi (transposition cipher)
Pada cipher transposisi, huruf-huruf di dalam plainteks tetap saja, hanya saja urutannya diubah. Dengan kata lain algoritma ini melakukan transpose terhadap rangkaian karakter di dalam teks. Nama lain untuk metode ini adalah permutasi atau pengacakan (scrambling) karena transpose setiap karakter di dalam teks sama dengan mempermutasikan karakter-karkater tersebut. (Munir.2006)

Jenis Kriptografi Klasik

Vigènere cipher

Vigenere cipher mungkin adalah contoh terbaik dari cipher alphabet-majemuk ‘manual’. Algoritma ini dipublikasikan oleh diplomat (sekaligus seorang kriptologis) perancis, Blaise de Vigènere pada abad 16. Vigènere cipher dipublikasikan pada tahun 1586. Cipher ini berhasil dipecahkan oleh Babbage dan Kasiski pada pertengahan abad 19. Vigènere cipher digunakan oleh tentara Konfiderasi (Confederate Army) pada perang sipil Amerika (American Civil war).

Vigènere cipher sangat dikenal karena mudah dipahami dan diimplementasikan. Cipher menggunakan bujursangakar Vigènere untuk melakukan enkripsi. Kolom paling kiri dari bujursangkar menyatakan huruf-hurf kunci, sedangkan baris paling atas menyatakan huruf-huruf plainteks. Setiap baris dalam bujursangkar menyatakan huruf-huruf cipherteks, yang mana jumlah pergesaran huruf plainteks ditentukan nilai numerik huruf kunci tersebut ( yaitu, A = 0, B = 1, C = 2,…, Z = 25). Bujursangkar vigènere digunakan untuk memperoleh cipherteks dengan menggunakan kunci yang sudah ditentukan. Jika panjang kunci lebih pendek dari pada panjang plainteks, maka kunci diulang penggunaanya (sistem periodik). Bila panjang kunci adalah m, maka periodenya dikatakan m. sebagai contoh, jika plainteks adalah THIS PLAINTEXT dan kunci adalah sony maka penggunaan kunci secara periodik adalah sebagai berikut:

         Plainteks      : THIS PLAINTEXT

         Kunci          : SONY SONYSONYS

         Cipherteks   : LVVQ HZNGFHRVL

Autokey Cipher

Kriptografi Autokey adalah pengembangan dari kriprografi Caesar dan Vigenere. Cara  melakukan enkripsi sama seperti kedua  kriptografi  sebelumnya. Pada kriptografi  Autokey  juga  digunakan sebuah kata sebagai kunci. Kunci ini kemudian diikuti dengan plaintext sehingga  membentuk  huruf-huruf yang sama panjang dengan plaintext. Urutan huruf-huruf ini yang akan digunakan sebagai kunci pada saat  enkripsi. Rumus yang berlaku  untuk  kriptografi Autokey sama seperti Caesar dan Vigenere.

Contoh, jika plaintext adalah INI PESAN RAHASIA, maka jika kita gunakan kunci kata BESOK, maka kata BESOK akan disisipkan di depan plaintext INI PESAN RAHASIA. Kemudian enkripsi dilakukan sama dengan enkripsi Caesar dan Vigenere.

 Reverse Cipher

Ini aadalah contoh kriptografi klasik yang menggunakan substitusi yaitu mengganti satu huruf dengan  huruf  lain ataupun mengubah suatu kalimat dengan menuliskan setiap kata secara terbalik. Ini contoh yang paling sederhana dari transposisi yaitu mengubah suatu kalimat dengan menuliskan setiap kata secara terbalik. Contoh Kriptografi Reverse:

Plaintext    : AKU AKAN PERGI BESOK PAGI

Ciphertext : UKA NAKA IGREP KOSEB IGAP

Pada kriptografi kolom (column cipher), plaintext disusun dalam kelompok huruf yang terdiri dari beberapa huruf. Kemudian huruf-huruf  dalam kelompok ini dituliskan kembali kolom per kolom, dengan urutan kolom yang bisa berubah-ubah. Contoh Kriptografi Kolom:

Kalimat ‘ AYAH SUDAH TIBA KEMARIN SORE ’, jika disusun dalam kolom 7 huruf, maka akan menjadi kolom - kolom berikut :

AYAHSUD
AHTIBAK

EMARINS

OREAAAA

Untuk melengkapi kolom terakhir agar berisi 7 huruf, maka sisanya diisi dengan huruf ‘A’atau bisa huruf apa saja sebagai huruf pelengkap. Kalimat tesebut setelah dienkripsi dengan 7 kolom huruf dan urutan kunci 6725431, maka hasil enkripsinya:

DKSAATAEUANASBIAHIRAAAEOYHMR

Zig-Zag Cipher

Pada  kriptografi  kolom  zig-zag, plaintext  disusun  dalam  kelompok  huruf yang  terdiri  dari beberapa huruf. Kemudian huruf-huruf dalam uruta kolom yang dimasukkan secara pola zig-zag.

Segitiga Cipher

Pada kriptografi  kolom Triangle, plaintext disusun  dalam  kelompok huruf yang terdiri dari  beberapa huruf. Kemudian huruf-huruf dalam urutan kolom yang dimasukkan secara pola segitiga.

Super Enkripsi

Kombinasi Antara Cipher Substitusi (Caesar Cipher) dan Cipher Tranposisi (Column Cipher). Sehingga memperoleh Cipher yang lebih kuat (Super) dari pada Satu Cipher saja.

Enigma Machine

Enigma Machine adalah mesin yang digunakan Jerman selama Perang Dunia II untuk mengenkripsi/dekripsi pesan-pesan militer. Enigma menggunakan sistem rotor(mesin berbentuk  roda  yang  berputar) untuk membentuk huruf  cipherteks  yang berubah - ubah. Setelah setiap huruf  dienkripsi, rotor kembali berputar untuk membentuk huruf cipherteks yang baru.

Jenis-Jenis Kriptografi

Algoritma kriptografi dibagi menjadi tiga bagian berdasarkan kunci yang dipakainya :

1. Kriptografi Simetris

Pengertian Kriptografi Simetris

Kriptografi Simetris adalah : Kode Hill atau lebih dikenal dengan Hill cipher merupakan salah satu algoritma kriptografi kunci simetris dan merupakan salah satu kripto polyalphabetic. Hill cipher diciptakan oleh Lester S. Hill pada tahun 1929 .

Teknik kriptografi ini diciptakan dengan maksud untuk dapat menciptakan cipher yang tidak dapat dipecahkan menggunakanteknik analisis frekuensi. Berbeda dengan caesar cipher, hill cipher tidak mengganti setiap abjad yang sama pada plainteks dengan abjad lainnya yang sama pada cipherteks karena menggunakan perkalian matriks pada dasar enkripsi dan dekripsinya.
Hill cipher merupakan penerapan aritmatika modulo pada kriptografi. Teknik kriptografi ini enggunakan sebuah matriks persegi sebagai kunci berukuran m x m sebagai kunci untuk melakukan enkripsi dan dekripsi. Dasar teori matriks yang digunakan dalam Hill cipher antara lain adalah perkalian antar matriks dan melakukan invers pada matriks
Karena menggunakan matriks sebagai kunci, Hill cipher merupakan algoritma kriptografi kunci simetris yang sulit dipecahkan, karena teknik kriptanalisis seperti analisis frekuensi tidak dapat diterapkan dengan mudah untuk memecahkan algoritma ini. Hill cipher sangat sulit dipecahkan jika kriptanalis hanya memiliki ciphertext saja (chipertext-only), namun dapat dipecahkan dengan mudah jika kriptanalis memiliki ciphertext dan potongan dari plaintext-nya (known-plaintext).

Gambar Kriptografi Simetris :

Gambar Kriptografi Simetris

Cara Enkripsi

Dengan mengkodekan atau mengubah setiap huruf abjad dengan integer sebagai berikut: A = 0, B = 1, …, Z = 25

Cara Enkripsi

maka secara matematis, proses enkripsi pada hill cipher adalah:

C = K . P mod 26
C = Cipherteks | K = Kunci | P = Plainteks

Proses enkripsi pada hill cipher dilakukan per blok plainteks. Ukuran blok tersebut sama dengan ukuran matriks kuncinya. Perhatikan contoh dibawah ini!

P = D O D I S P U T R A ,dikodekan/diintegerkan menjadi
P = 3 14 3 8 18 15 20 19 17 0

2. Kriptografi Asimetris

Pengertian Kriptografi Asimetris

Algoritma asimetris, sering juga disebut dengan algoritma kunci publik atausandi kunci publik, menggunakan dua jenis kunci, yaitu kunci publik (public key) dan kunci rahasia (secret key). Kunci publik merupakan kunci yang digunakan untuk mengenkripsi pesan. Sedangkan kunci rahasia digunakan untuk mendekripsi pesan.
Kunci publik bersifat umum, artinya kunci ini tidak dirahasiakan sehingga dapat dilihat oleh siapa saja. Sedangkan kunci rahasia adalah kunci yang dirahasiakan dan hanya orang-orang tertentu saja yang boleh mengetahuinya. Keuntungan utama dari algoritma ini adalah memberikan jaminan keamanan kepada siapa saja yang melakukan pertukaran informasi meskipun di antara mereka tidak ada kesepakatan mengenai keamanan pesan terlebih dahulu maupun saling tidak mengenal satu sama lainnya.

Gambar Kriptografi Asimetris

Gambar Kriptografi Asimetris

3. Kriptografi Hibrid

Pengertian Kriptografi Hibrid

Permasalahan yang menarik pada bidang kemanan informasi adalah adanya trade off antara kecepatan dengan kenyamanan. Semakin aman semakin tidak nyaman, berlaku juga sebaliknya semakin nyaman semakin tidak aman. Salah satu contohnya adalah bidang kriptografi. Tetapi hal ini dapat diatasi dengan penggunaan kriptografi hibrida. Kriptografi hibrida sering dipakai karena memanfaatkan keunggulan kecepatan pemrosesan data oleh algoritma simetrik dan kemudahan transfer kunci menggunakan algoritma asimetrik. Hal ini mengakibatkan peningkatan kecepatan tanpa mengurangi kenyamanan serta keamanan. Aplikasi kriptografi hibrida yang ada saat ini pada umumnya ditujukan untuk penggunaan umum atau mainstream yang merupakan pengguna komputer.

Aplikasi pada umumnya mengikuti perkembangan hardware komputer yang semakin cepat dari waktu ke waktu. Sehingga hardware yang sudah lama tidak dapat difungsikan sebagaimana mestinya. Selain itu banyak perangkat embedded dengan kekuatan pemrosesan maupun daya yang terbatas. Terutama dengan trend akhir akhir ini, hampir semua orang memiliki handheld device yang mempunyai kekuatan terbatas, seperti telepon seluler.
Dalam tugas akhir ini dibahas mengenai perancangan sebuah aplikasi kriptografi hibrida yang ditujukan untuk kalangan tertentu, terutama pemakai hardware dengan kekuatan pemrosesan yang terbatas. Aplikasi yang ingin dicapai adalah aplikasi yang sederhana, ringan dan cepat tanpa mengurangi tingkat keamanan menggunakan hash.

Sistem ini mengggabungkan chiper simetrik dan asimetrik. Proses ini dimulai dengan negosiasi menggunakan chiper asimetrik dimana kedua belah pihak setuju dengan private key/session key yang akan dipakai. Kemudian session key digunakan dengan teknik chiper simetrik untuk mengenkripsi conversation ataupun tukar-menukar data selanjutnya. Suatu session key hanya dipakai sekali sesi. Untuk sesi selanjutnya session key harus dibuat kembali.

Gambar Kriptografi Hibrid

Gambar Kriptografi Hibrid

ENKRIPSI SUPER

SUPER ENKRIPSI

Read More